13日的讲座面向全系各专业的师生。他没有重复大爆炸理论已经取得的成就,而是着重于一个似乎无法解释的疑惑:宇宙是平的。
自从广义相对论面世以来,空间弯曲这个不容易理解的概念已经广为人知。在爱因斯坦这个理论中,质量告诉空间如何弯曲。地球之所以在绕着太阳公转,是因为太阳附近的空间是弯曲的,迫使地球随之拐弯。不过太阳的质量虽然很大,对宇宙来说却轻如鸿毛。一旦离开了太阳系,它的影响微乎其微,那外面的空间不会因太阳而弯曲。
当然,天外有天。宇宙有数不清的太阳,还有质量更大的中子星、黑洞等等。它们各行其责,令自己附近的空间弯曲,却也会同样地对遥远的空间无能为力。从整个宇宙这个大尺度来看,空间是弯曲的还是平坦的?
爱因斯坦在1917年给出的第一个宇宙模型时答曰:是弯曲的。那是一个“有限无边”的“球形奶牛”式宇宙。其中每一个点都有着同样的弯曲度,一个类似于二维球面的三维圆球。
弗里德曼、勒梅特等人很快发现爱因斯坦的模型只是一个特例,而且是他无中生有地引进那个宇宙常数、凑出一个静态宇宙的结果。如果没有那个宇宙常数项,广义相对论中的宇宙是随时间变化的,而余下的三维空间既可以是正曲率(类似于二维的球面)、负曲率(类似于二维的马鞍面),也可以就是寻常的、平坦的欧几里德空间。
在哈勃证明宇宙的膨胀之后,爱因斯坦放弃他的宇宙模型。宇宙的形状便再度成为悬而未决的课题。弗里德曼发现,爱因斯坦方程中的宇宙形状取决于其中的质量密度。如果密度恰好是某个特定的数值,那么宇宙就是平坦的。密度大了,宇宙会有正曲率;小了,则是负曲率。那个特定的数值便叫做“临界密度”(critical density)。为了方便,物理学家把宇宙的实际密度与临界密度之比叫做“欧米伽”(Ω)。只有在Ω等于1时,才会有一个平坦的宇宙。
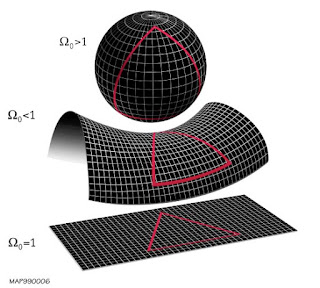 |
| 宇宙空间可能有的几何形状的二维示意图:参数Ω的数值大于1时,宇宙是正曲率的球面(上);小于1时,是负曲率的马鞍面(中);只有严格等于1时,才会有平坦的宇宙。 |
在1970年代,天文学家已经注意到远方星系的数量大致与距离成正比,表明我们所在的宇宙其实是平坦的。彭齐亚斯和威尔逊观察到的微波背景在天际的各个方向看不出区别,也说明宇宙的曲率——如果有的话——会非常之小。
对质量密度的估计也合拍:今天宇宙的Ω可能处于0.1与2之间,相当地接近1。
狄克在错失微波背景的发现后不久就开始思考这个问题,这时已经琢磨了近十年。他讲解道:Ω不是一个常数,会随着宇宙的膨胀变化。这是一个“放大”的过程:如果宇宙初始时Ω稍微大于1,它会变得越来越大;如果当初稍微小于1,它今天就应该已经变得非常小。只有从一开始Ω严格等于1,宇宙才会永久性地平坦。
Ω要具备今天接近于1的数值,它在大爆炸后的一分钟时必须介于0.999999999999999和1.000000000000001之间。如果说这是碰巧的话,我们的运气实在匪夷所思。狄克因此忧虑,大爆炸理论可能不完备,存在着明显的漏洞。
其实,类似的困惑不止这一个。还有一个挑战可以溯源于日常生活中不值一哂的常识:夜晚的天空是黑的。如何解释这个粗浅问题,曾经足足困扰了天文学家几百年。
曾几何时,夜晚的天空是黑的属于天经地义:在托勒密的描述中,恒星不过是稀稀疏疏地镶嵌在天球上的点缀。在没有太阳光的夜晚,天幕上自然只有那么些个繁星在闪烁。
当伽利略在17世纪初举起他自制的望远镜看到“不可思议之多”的、过去从来没有人看到过的满天星星时,人类才意识到肉眼所见的星星只是宇宙的一小部分。天外有天,也许会是无边无际。
开普勒立即为这个浪漫的想法当头浇了一盆冷水。他“一针见血”地指出,如果宇宙中有无穷无尽的星星,它们总体的光亮会接近甚至超过太阳。地球上便不可能有黑暗的夜空。
开普勒的想法由德国的居里克(Otto von Guericke)赋予更完整的描述。他形象地类比道:一个人如果身处无限的森林之中,无论林中的树木粗细、疏密,他都无法看到森林之外的亮光。因为无论往哪个方向看,他的视线迟早会被或远或近的某颗树挡住。只有在有限大小的森林中,才有可能通过树间的缝隙看到外面的光亮。
夜晚看天上的星星正好相反。如果有无限多的星星,那么无论在哪个方向都迟早会看到一颗在发光的星星。这样,即使在夜晚,星星的亮光应该完全覆盖整个天幕。
居里克以在他担任市长的城市中演示科学实验著名,尤其热衷于真空。他曾将两个密封的半球中间抽成真空,然后各用8匹强壮的马从两边拉,结果拉不开这两个半球,展示了大气压的威力。他认为,夜晚的黑暗说明宇宙中有星星的部分很有限。更远的地方是无限的真空,不再有星星。我们在星星之间看到的黑暗,便是那遥远真空的所在。
不料,居里克无意中给后来的牛顿出了个大难题。发现了万有引力的牛顿意识到,假如宇宙中只存在有限数目的星星,这些星星迟早会因为引力坍缩到一个点上。只有在无穷多的星星存在时,才能在各方向彼此抵消引力而平衡。(当然,牛顿这个论断也不成立:无穷多的星星保持平衡只是数学上的一个不稳定解,现实中不可能存在。)
于是,夜晚的天空为什么黑暗,依然无法解释。在那之后的几代天文学家相继提出各种解释,也都铩羽而归。
比如以计算出彗星回归而著名的哈雷(Edmond Halley)。他以光的波动说这个新理论计算恒星光的传播,指出光强会随距离的平方衰减。越远的星光到地球时越是微弱,这是我们无法用肉眼看到远处星星的原因。他认为也可以解释夜空的黑暗,因为太远的星星光亮太弱,没有贡献。
但我们看到星光并不是个体的星星,而是视线内所有星星光的总和。遗憾的是,哈雷在计算星星的分布时犯了一个几何上的错误。一个视角上的面积与距离的平方成正比,因此视角内一定距离上星星的数量也与距离的平方成正比。它们发光的总和正好抵消了衰减的损失,到达地球的光亮因此与距离无关。这样,即使我们分辨不出远处个体的星星,夜晚的天空还是会被无穷多的星星照亮——类似于我们看到的银河、星云中成片的光亮。
1848年,美国作家、诗人爱伦·坡(Edgar Allan Poe)突发奇想,在纽约举办了一个演讲会,发布他会对现代宇宙学“有革命性影响”的成果。现场听众寥寥无几,没有他所期望的宾客满堂。随后,他把演讲稿写成散文诗,题目叫做《尤里卡》(Eureka)。这个词来自传说中希腊科学家阿基米德(Archimedes)在澡盆中领悟到浮力原理时的兴奋叫喊:“我明白了”。
 |
| “发现”夜晚的天空为什么黑暗的诗人爱伦·坡。 |
爱伦·坡此前听过一两次科学讲座,也读了几本相关的书。但他只是以诗人的情怀描述他所理解的客观世界。他“看到”宇宙随着神灵心跳的节奏不断膨胀、收缩,他预见宇宙最终将走向毁灭……在丰富多彩的浪漫想象中,他也写道:如果宇宙中有无限多的星星,那么黑夜一定会光明得如同白昼。我们之所以有黑夜,唯一的可能是遥远的星光还没来得及抵达地球。
《尤里卡》出版后依然石沉大海,毫无反响。一年后,爱伦·坡在贫困、酗酒、潦倒中去世,享年仅40岁。作为艺术家,他在死后获得了比生前辉煌得多的名声。
就在《尤里卡》问世的那一年,年仅24岁的英国剑桥的物理学家汤姆森(William Thomson)推出了后来成为科学标准的“绝对温标”(absolute temperature)。(汤姆森后来封爵而改称开尔文勋爵(Lord Kelvin)。绝对温标的单位也被叫做“开尔文”(K)。我们现在所说的宇宙微波背景辐射的温度用的就是这个温标。)1884年,已经是大师的汤姆森来到爱伦·坡生前居住的巴尔的摩市,应邀在成立不久的约翰斯·霍普金斯大学给那时还处于蛮荒状态的美国物理学界做一系列讲座。他们不知道爱伦·坡那“越界”的诗篇,但汤姆森在讲座中介绍了他自己对夜空黑暗问题的研究。
与爱伦·坡不谋而合的是,汤姆森也认为很多恒星的光没能传到地球。但作为科学家,他依据的不仅仅是想象。那时的物理学家已经知道恒星发光需要消耗燃料,因此不可能永远地发光。当我们观看几亿光年之外时,那里的恒星不可能连续发光几亿年。如果它们与太阳的寿命同步,它们现在是在发光,但那光还没来得及到达地球。
这样,我们能看到的不是宇宙所有的星星,而只是其中一小部分。汤普森把这部分叫做“可见宇宙”(visible universe),并做了相应的估算。因为可见的星星是有限的,像一个不那么大的森林一样,我们可以通过缝隙看到夜空的黑暗。
他在偏僻的美国所做的这个报告也没引起过多大注意。
及至1950年代,也是在剑桥的邦迪提出合理地解释夜空的黑暗是天文学的重要职责。他发表了一系列论文,还把这个历史难题“正式”命名为“奥伯斯佯谬”(Olbers' paradox)。奥伯斯(Heinrich Olbers)是19世纪初曾参与该争论的一个德国天文爱好者。但他既不是这“佯谬”的提出者,也没有什么突出的贡献。
邦迪之所以旧话重提,是因为他发现夜空的黑暗其实是宇宙膨胀的证据:因为越远的恒星膨胀的速度越快,它们发出的光红移得越厉害,可能完全移出可见光频段,因此在夜晚看不见。这个解释对他尤其合适,因为可以符合他那个无限、稳定态宇宙模型。
然而,还是后来击溃了稳定态宇宙的大爆炸理论能够给出更扎实、准确的描述。
在大爆炸之初,宇宙曾经充满了光。但那时的光子与质子、电子等基本粒子组成的高温等离子体搅和在一起,并不透明。只有在30万年、质子与电子组合成稳定的原子之后,才出现第一缕可见的光。时至今日,那些光子已经红移到微波频段,只能用贝尔实验室的喇叭天线才能“看到”,但不再为我们的夜空提供任何光亮。
后来,宇宙还经历过“黑暗时代”,才有了第一代恒星的诞生。这些以及后来出现的恒星距离我们会更近一些,它们发出的光也还没有完全被红移,能够被现代天文望远镜捕捉到。它们是最早——也就是最远——的恒星。在它们之外不再有光。于是,从地球上仰望,夜空中没有布满闪烁的星星,而是存在大量的“缝隙”,便是没有光亮的黑幕。
爱伦·坡和汤普森不可能知道宇宙会有一个年龄、时间会有一个起点,否则他们那个“远处星星的光还没来得及传到地球”会更有说服力。他们误打误撞的解释虽然也不尽正确,却在不经意中引入了一个重要的物理概念。
因为他们也不可能想到的是,20世纪初的爱因斯坦会提出一个惊人的思想:宇宙中传递信息的速度不可能超过光速,并由此发展出相对论。如果在宇宙有限的年龄中,某个地方的光还来不及传播到地球来,那么地球上的人类便不可能获知那个地方的任何信息。对于地球人来说,那不只是看不见那里可能有的星星,而是那个地方本身不具备任何物理意义、无法定义其是否存在。
于是,汤普森的“可见宇宙”可以推广为“可观测宇宙”(observable universe):人类所能认知的宇宙,只是与地球能以光传播发生联系的那部分。在那之外,是否依然天外有天、宇宙是有限还是无限……凡此种种,都因为无法认知而“无所谓”了。
我们在地球上登高望远,视线会因为地理的阻挡有一个极限,叫做地平线。相应地,当我们仰望星空时,也会遭遇到这个“可观测宇宙”的极限,在天文中也叫做“视界”(visible horizon)。在今天的宇宙,这个视界的距离大致——但不完全——等于光速乘以宇宙的年龄,即从大爆炸伊始到今天光所能传播的最远距离。
细心的天文学家便由此发现了宇宙的另一个蹊跷。
我们在地球上往东看,在接近视界的距离上观测到了微波背景辐射。我们转过身来再往西看,也是在接近视界的距离观测到了微波背景辐射。它们都在我们的视界之内。但是,因为它们各自在相对的两个方向,彼此之间便间隔了接近两个视界的距离。从宇宙大爆炸到今天,光——或任何信息——不可能从其中一边传递到另一边。
不仅如此。微波背景辐射的光子出现在宇宙大爆炸后“仅仅”30万年的时候。那时的宇宙更年轻,视界比现在还短太多。所以,东边的微波光子与西边的微波光子从来不可能建立过联系、交换过信息。
 |
| “视界问题”示意图。我们看到的微波背景辐射是在宇宙大爆炸后30万年时发出的。那时的光和信息只来得及传播到图中两个小圆圈所标的范围。两个小圆圈之间不可能互相交流。 |
然而,无论从哪个方向来的微波光子都有着同样的频率、处于同一温度。它们是怎么约好——物理行话叫“达到热平衡”——的?
也许与宇宙是平的一样,这又是碰巧了。我们的宇宙会有那么多诡秘的巧合吗?难怪狄克教授会对大爆炸理论的可靠性深为忧虑。
狄克那天在康奈尔讲座的教室里坐着一位年轻的博士后。他对广义相对论、宇宙学只有泛泛的了解。那天他得了支气管炎正在发烧,只是懵懵懂懂地听了狄克的讲述,在日记里简单记下了这个挺有意思的问题。因为这些与他正在进行的研究完全不搭界,他没有再去琢磨。
他完全不知道,仅仅不到2年,他会成为在解决大爆炸理论这两个难题上做出重大突破的先驱。
(待续)
科普


